灵神常见算法

2019年

第 8 题

一棵二叉树如右图所示，若采用顺序存储结构，即用一维数组元素存储该二叉树中的结点（根结点的下标为 1，若某结点的下标为 i，则其左孩子位于下标 2i 处、右孩子位于下标2i+1 处），则该数组的最大下标至少为（）。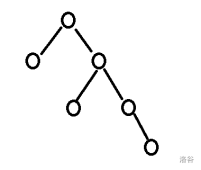

A. 6

B. 10

C. 15

D. 12

选C。

第 14 题

假设一棵二叉树的后序遍历序列为 DGJHEBIFCA，中序遍历序列为 DBGEHJACIF，则其前序遍历序列为（）。

A. ABCDEFGHIJ

B. ABDEGHJCFI

C. ABDEGJHCFI

D. ABDEGHJFIC

选B。

graph TB
    A --> B & C
    B --> D & E
    E --> G & H
    H --> J

    C --> S((NULL)) & F
    F --> I & Q((NULL))

graph TB ​ A --> B & C ​ B --> D & E ​ E --> G & H ​ H --> J ​ C --> S((NULL)) & F ​ F --> I & Q((NULL))

2020年

第 12 题

独根树的高度为 1。具有 61 个结点的完全二叉树的高度为（ ）。

A. 7

B. 8

C. 5

D. 6

选D。

解析：根据二叉树的性质，由于高度h的满二叉树共有$2^{h}-1$个结点，所以满二叉树的高度为 $\log_2(n+1)$，其中 n 为结点个数。

• 高度h的完全二叉树至少有$2^{h-1}$个结点
• 高度h的完全二叉树至多有$2^h-1$个结点.

因此，具有 61 个结点的完全二叉树的高度为 $\lfloor \log_2(61) \rfloor + 1 = \lfloor \log_2(61) \rfloor + 1 = 6$。

第1层有1个结点，第2层有2个结点，第3层有4个，每次都是乘2，从二进制数的角度看，就是左移一位。

第1层有1个结点，第2层有10个结点，第3层有100个。

高度为2的满二叉树共有 1 + 10 = 11 个结点，高度为3的满二叉树共有 100 + 11 = 111 个结点。

2021年

第 8 题

如果一棵二叉树只有根结点，那么这棵二叉树高度为 1。请问高度为 5 的完全二叉树有 （ ）种不同的形态？

A. 16

B. 15

C. 17

D. 32

A。高度为5，有2^5 = 16个节点，最后一层可以有0~16个节点，有16种形态。

2022年

第 7 题

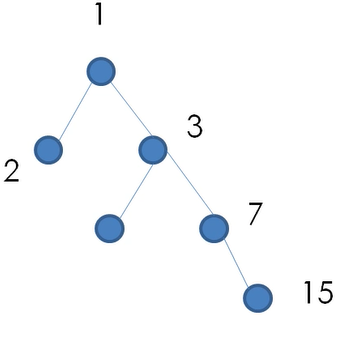
假设字母表 ｛a,b,c,d,e｝ 在字符串出现的频率分别为 10%，15%，30%，16%，29%。若使用哈夫曼编码方式对字母进行不定长的二进制编码，字母 d 的编码长度（ ）位。

A. 1

B. 2

C. 2 或 3

D. 3

选B。构造哈夫曼树，每次选最小的两个数，合成一个新节点。

到达d节点的路径为0 0，长度为2。

第 8 题

一棵有 n 个结点的完全二叉树用数组进行存储与表示，已知根结点存储在数组的第 1 个位置。若存储在数组第 9 个位置的结点存在兄弟结点和两个子结点，则它的兄弟结点和右子结点的位置分别是（ ）。

A. 8、18

B. 10、18

C. 8、19

D. 10、19

选C。

• 9是奇数，是右子节点，兄弟节点在左边。
• 左子2 * x，右子2 * x + 1，9的右子节点位置为2 * 9 + 1 = 19。