2021年CSP-J1真题
发表于：2023-08-12 | 分类： CSP
字数统计: 3k | 阅读时长: 13分钟 | 阅读量：

一、单向选择题

第 1 题
以下不属于面向对象程序设计语言的是（ ）。

A. C++

B. Python

C. Java

D. C

选D。C语言没有对象，是面向过程语言。

第 2 题
以下奖项与计算机领域最相关的是（ ）。

A. 奥斯卡奖

B. 图灵奖

C. 诺贝尔奖

D. 普利策奖

选B。

第 3 题
目前主流的计算机储存数据最终都是转换成（ ）数据进行储存。

A. 二进制

B. 十进制

C. 八进制

D. 十六进制

选A。

第 4 题
以比较作为基本运算，在 N 个数中找出最大数，最坏情况下所需要的最少的比较次数为 （ ）。

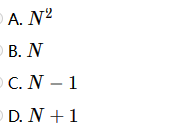
image-20230812160644484

选C。第一个数跟第二个数比，大的跟第三个数比，一共比 N - 1 次。

第 5 题
对于入栈顺序为 a,b,c,d,e 的序列，下列（ ）不是合法的出栈序列。

A. a,b,c,d,e

B. e,d,c,b,a

C. b,a,c,d,e

D. c,d,a,e,b

选D。

flowchart LR AA("出栈顺序 --- ​ 栈") --> A(" --- ​ c ​ b a") -->|c出栈| B("c --- ​ b a") -->|d入栈| C("c --- ​ d ​ b a") -->|d出栈| D("c d --- ​ b ​ a") --> |a出栈| E(a不在栈顶,错误) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
flowchart LR
	 AA("出栈顺序
      ---
      	栈") --> 
      A("
      ---
      	c
        b
        a") -->|c出栈| B("c
        ---
        b
        a") -->|d入栈| C("c
        ---
        d
        b
        a") -->|d出栈| D("c d
        ---
        b
        a") --> |a出栈| E(a不在栈顶,错误)

第 6 题
对于有 n 个顶点、m 条边的无向连通图 (m>n)，需要删掉（ ）条边才能使其成为一棵树。

A. n − 1

B. m − n

C. m − n − 1

D. m − n + 1

选D。树有n - 1条边，把这个图变成树，即变成n - 1条边，需要删掉 m - (n - 1) = m - n + 1 条边。

第 7 题
二进制数101.11 对应的十进制数是（ ）。

A. 6.5

B. 5.5

C. 5.75

D. 5.25

选C。

$$
12^2+12^0+12^{-1}+12^{-2} = 5.75
$$

第 8 题

如果一棵二叉树只有根结点，那么这棵二叉树高度为 1。请问高度为 5 的完全二叉树有 （ ）种不同的形态？

A. 16

B. 15

C. 17

D. 32

A。高度为5，有2^5 = 16个节点，最后一层可以有0~16个节点，有16种形态。

第 9 题
表达式 a*(b+c)*d 的后缀表达式为( )，其中*和 +是运算符。

A. **a+bcd

B. abc+*d*

C. abc+d**

D. *a*+bcd

选B。

1
2
3
4
(b + c) 变成 (b c +) 
a * (b c +) 变成 a (b c +) *
a (b c +) * * d 变成 a (b c +) * d *
去掉括号 a b c + * d *

第 10 题
6 个人，两个人组一队，总共组成三队，不区分队伍的编号。不同的组队情况有（ ）种。

A. 10

B. 15

C. 30

D. 20

选B。6取2，剩下4取2，剩下2取2，队伍没有顺序，要除以三个队伍的排列数。

$$
C_6^2 * C^2_4 * C^2_2 / A_3^3 = 15
$$

第 11 题

在数据压缩编码中的哈夫曼编码方法，在本质上是一种（ ）的策略。

A. 枚举

B. 贪心

C. 递归

D. 动态规划

选B。在数据压缩编码中的哈夫曼编码方法，是一种贪心算法，它的基本思想是：在编码过程中，优先选择使编码总长度最短的符号。

第 12 题

由 1,1,2,2,3 这五个数字组成不同的三位数有（ ）种。

A. 18

B. 15

C. 12

D. 24

选A。依次枚举：

1开头：112、113、121、122、123、131、132

2开头：211、212、213、221、223、231、232

3开头：311、312、321、322

第 13 题

考虑如下递归算法

1
2
3
4
solve(n)  
     if n<=1 return 1  
     else if n>=5 return n*solve(n-2)  
     else return n*solve(n-1)

则调用 solve(7) 得到的返回结果为（ ）。

A. 105

B. 840

C. 210

D. 420

选C。7 * 5 * 3 * 2 * 1 = 210。

第 14 题

以 a 为起点，对下边的无向图进行深度优先遍历，则 b,c,d,e 四个点中有可能作为最后一个遍历到的点的个数为（ ）。

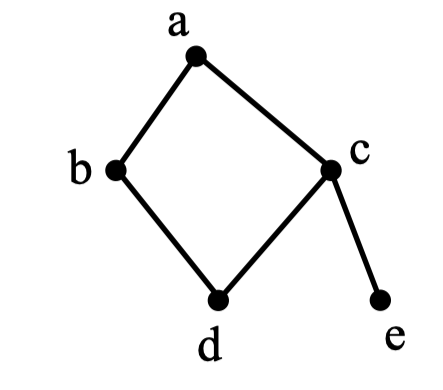
image-20230827215903496

A. 1

B. 2

C. 3

D. 4

选B。b和e可能为最后一个点。

第 15 题

有四个人要从 A 点坐一条船过河到 B 点，船一开始在 A 点。该船一次最多可坐两个人。 已知这四个人中每个人独自坐船的过河时间分别为 1,2,4,8，且两个人坐船的过河时间为两人独自过河时间的较大者。则最短（ ）时间可以让四个人都过河到 B 点（包括从 B 点把船开回 A 点的时间）。

A. 14

B. 15

C. 16

D. 17

选B。

1 号和 2 号过河，花费 2 分钟。

1 号回来，花费 1 分钟。

4 号和 8 号过河，花费 8 分钟。

2 号回来，花费 2 分钟。

1 号和 2 号再次过河，花费 2 分钟。

二、阅读程序

（1）

img

f函数统计1的个数，负数统计补码中1的个数。如下图（2018年考过该算法）

g函数返回x的最低位（lowbit）。

image-20230812173934102

16.输入的 n 等于 1001 时，程序不会发生下标越界。（ 错 ）

a的下标0~999，1001越界。

17.输入的 a[i] 必须全为正整数，否则程序将陷入死循环。（ 错 ）

找一个反例即可，如0、-1。

18.当输入为 5 2 11 9 16 10 时，输出为 3 4 3 17 5。（ 错 ）

输出最后一个数错误，为4。

19.当输入为 1 511998 时，输出为 18。（ 对 ）

20.将源代码中 g 函数的定义（14∼17 行）移到 main 函数的后面，程序可以正常编译运行。（ 错 ）

前面得声明函数g，才能正常运行。

21.当输入为 2 -65536 2147483647 时，输出为（ B ）。

A. 65532 33
B. 65552 32
C. 65535 34
D. 65554 33

65536为2^16。1后面16个0，int32位，补码：1后面16个0不变，前面全变成1，有16个1。

最低位，1后面16个0。

65536 + 16 = 65552。

2147483647是2^31-1，有31个1，最低位为1。

31 + 1 = 32。

（2）

img

22、输出的第二行一定是由小写字母、大写字母、数字和 ++、 //、== 构成的字符串。（ 错 ）

输入编码以外的字符，即大小写字母、数字、+、/、=，输出乱码。

23、可能存在输入不同，但输出的第二行相同的情形。（ 正确 ）

24、输出的第一行为 -1。（ 正确 ）

char 是 signed char，强转int要补符号位。

0xff –> 0xffffffff，是-1的补码。

25、设输入字符串长度为 n，decode 函数的时间复杂度为（ ）

A. O(n)

B. O(n)

C. O(nlogn)

D. O(n2)

选B。循环n / 4次。

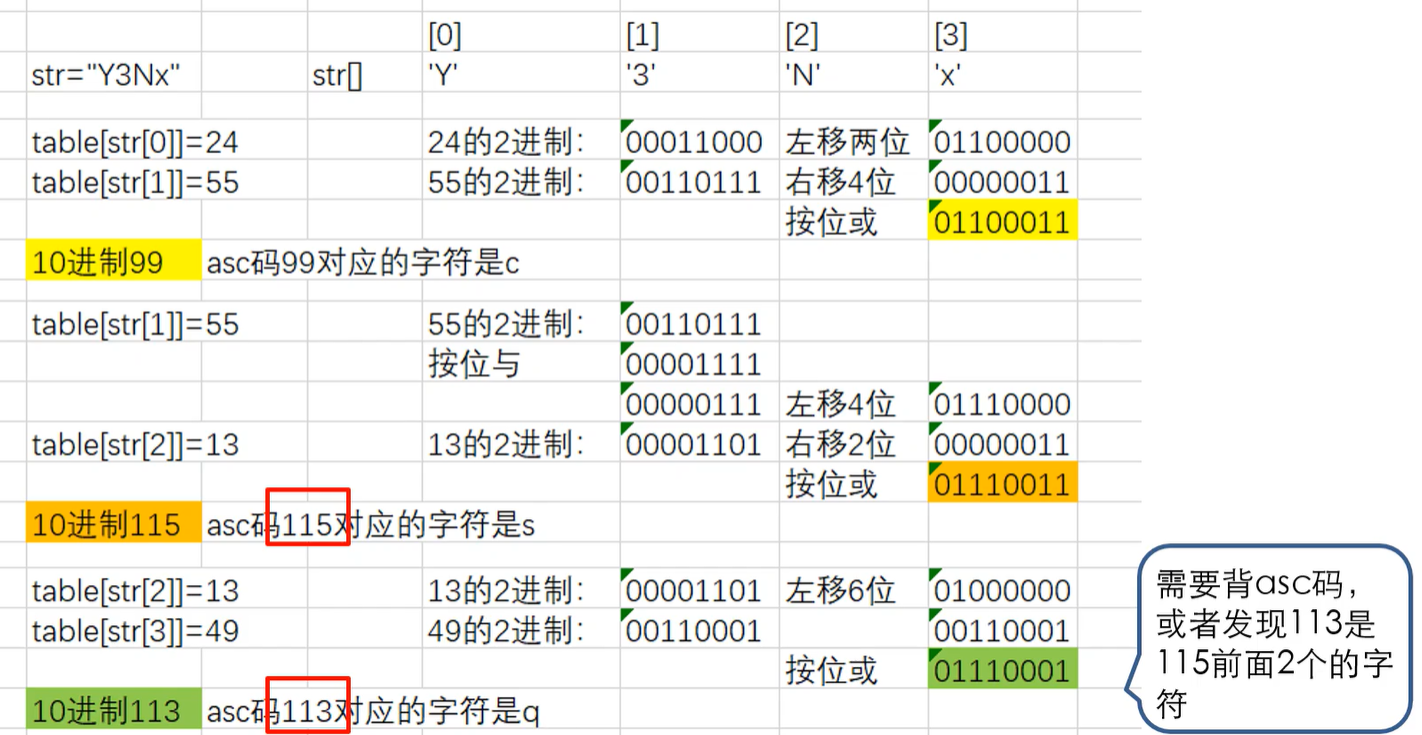
26、当输入为 Y3Nx 时，输出的第二行为（）。

A. csp

B. csq

C. CSP

D. Csp

选B。

image-20230813180142572

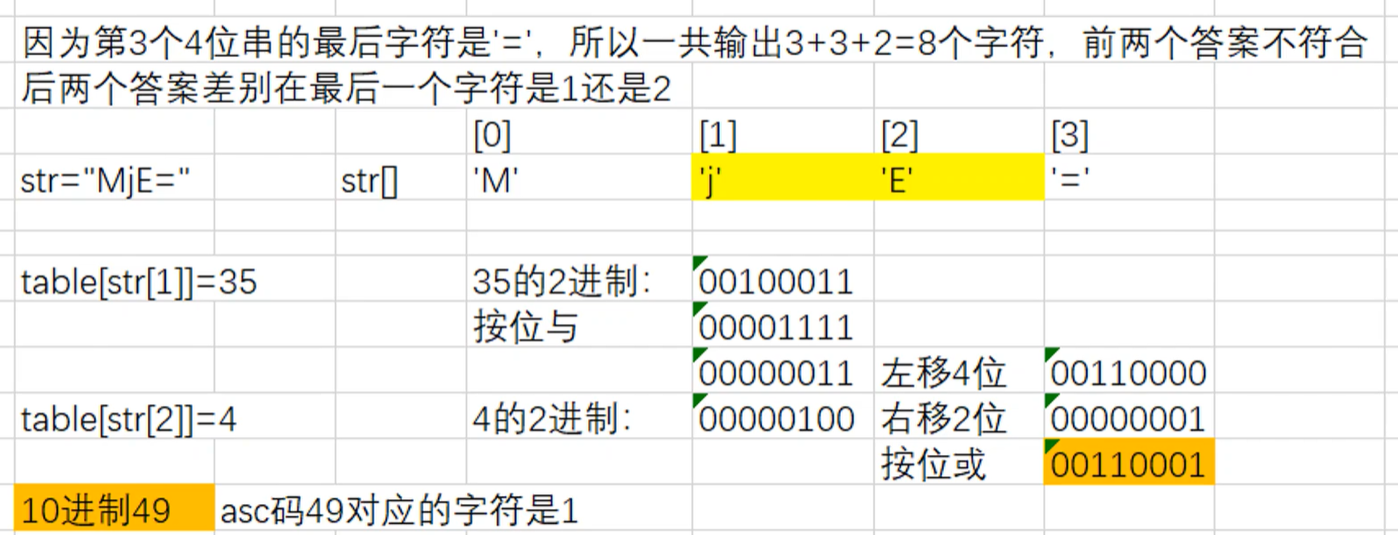
27、（3.5 分）当输入为 Y2NmIDIwMjE= 时，输出的第二行为（ ）。

A. ccf2021

B. ccf2022

C. ccf 2021

D. ccf 2022

选C。

image-20230813180359031

image-20230813180711143

（3）

img img

假设输入的 x 是不超过 1000 的自然数，完成下面的判断题和单选题：

线性筛质数，筛法 - OI Wiki (oi-wiki.org)

28、若输入不为 1，把第 13 行删去不会影响输出的结果。（ 正确 ）

循环从2开始。

29、第 25 行的 f[i] / c[i * k]可能存在无法整除而向下取整的情况。 （ 错误 ）

30、在执行完 init() 后，f 数组不是单调递增的，但 g 数组是单调递增的。 （ 错误 ）

g[i]是i的约数和，如果是质数，则gl]值会较小。比如g[5] = 1+5=6,而g[4] = 1+2+4=7。

31、init 函数的时间复杂度为（ ）。

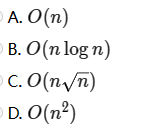
image-20230813181008222

选A。线性筛，复杂度为O(n)。

32、在执行完 init() 后，f*[1],f[2],f[3]…f[100] 中有（ ）个等于 2。

A. 23

B. 24

C. 25

D. 26

选C。约数只有1和自己，即质数，100以内的质数有25个。

33、（4 分） 当输入为 1000 时，输出为（）。

A. 15 1340

B. 15 2340

C. 16 2340

D. 16 1340

$$
1000 = 2^3 * 5^3
$$

选C。f[1000] = (1+3)*(1+3)=16

``g[1000] = (1+2+4+8)(1+5+25+125)=15156=2340`

三、完善程序

（1）Josephus 问题

有 n 个人围成一个圈，依次标号 0 至 n−1。从 00 号开始，依次 0,1,0,1,…交替报数，报到 1 的人会离开，直至圈中只剩下一个人。求最后剩下人的编号。

试补全模拟程序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;

const int MAXN = 1000000;
int F[MAXN];

int main(){
    int n;
    cin >> n;
    int i = 0, p = 0, c = 0;
    while (①) {
        if(F[i] == 0){
            if(②) {
                F[i] =1;
                ③;
            }
            ④;
        }
        ⑤;
    }
    int ans = -1;
    for (i =0;i < n; i++)
        if(F[i] ==0)
            ans = i;
    cout << ans << endl;
    return 0;	
}

34、①处应填（ ）
A.i < n
B.c < n
C.i < n- 1
D.c < n-1

选D。变量c表示离开的人数，假设n为3，c=2时就停止，故选c < n - 1

35、②处应填（ ）
A.i % 2 == 0
B.i % 2 == 1
C.p
D.!p

选C。变量p表示报数，报到1就离开，F[i]赋值为1。

36、③处应填（ ）
A.i++
B.i = (i + 1) % n
C.c++
D.p ^= 1

选C。报到1，离开的人数+1。

37、④处应填（ ）
A.i++
B.i = (i + 1) % n
C.c++
D.p ^= 1

选D。异或，下一个人报数 从0变1 或 从1变0。如果第i人离开了，报数p不变，故在if(F[i] == 0)内。

38、⑤处应填（ ）
A.i++
B.i = (i + 1) % n
C.c++
D.p ^= 1

选B。if(F[i] == 0)猜出i为下标。一圈数完后，从第一个人开始，所以要% n。

（2）矩形计数

平面上有 n 个关键点，求有多少个四条边都和 x 轴或者 y 轴平行的矩形，满足四个顶点都是关键点。给出的关键点可能有重复，但完全重合的矩形只计一 次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <iostream>

using namespace std;

struct point {
	int x, y, id;
};

bool equals(point a, point b) {
	return a.x == b.x && a.y == b.y;
}

bool cmp(point a, point b) {
	return ①;
}

void sort(point A[], int n){
	for (int i = 0; i < n; i++)
		for (int j = 1; j < n; j++)
			if (cmp(A[j], A[j - 1])) {
				point t = A[j];
				A[j] = A[j - 1];
				A[j- 1] = t;
            }
}

int unique(point A[],int n){
    int t = 0;
    for (int i = 0; i < n; i++)
    	if(②)
    		A[t++] = A[i];
    return t;
}

bool binary_search(point A[], int n, int x, int y){
    point p;
    p.x = x;
    p.y = y;
    p.id = n;
    int a = 0, b = n - 1;
    while (a < b) {
        int mid = ③;
        if(④)
            a = mid + 1;
        else
            b = mid;
    }
    return equals(A[a], p);
}
    
const int MAXN = 1000;
point A[MAXN];

int main(){
    int n;
    cin >> n;
    for(int i = 0; i < n; i++){
        cin >> A[i].× >> A[i].y;
        A[i].id = i;
    }
    sort(A, n);
    n = unique(A, n);
    int ans = 0;
    for (int i = 0; i < n; i++)
   		for (int j = 0; j < n; j++)
    		if (⑤ && binary_search(A, n, A[i].x, A[j].y) && 
                binary_search(A, n, A[j].x,A[i].y)) {
    		ans++;
            }
    cout << ans << endl;
    return 0;
}

试补全枚举算法。

39、①处应填 ( )
A. a.x != b.x ? a.x < b.x : a.id < b.id
B. a.x != b.x ? a.x < b.x : a.y < b.y
C. equals(a, b) ? a.id < b.id : a.x < b.x
D. equals(a, b) ? a.id < b.id : (a.x != b.x ? a.x < b.x : a.y < b.y)

选B。两点比较大小。

40、②处应填 ( )
A. i == 0 || cmp(A[i], A[i - 1])
B. t == 0 || equals(A[i], A[t - 1])
C. i == 0 || !cmp(A[i], A[i - 1])
D. t == 0 || !equals(A[i], A[t - 1])

选D。去重，双指针。

41、③处应填 ( )
A. b - (b - a) / 2 + 1
B. a + (b + 1) >> 1
C. (a + b) >> 1
D. a + (b - a + 1) / 2

选C。二分。

42、④处应填 ( )
A. !cmp(A[mid], p)
B. cmp(A[mid], p)
C. cmp(p, A[mid])
D. !cmp(p, A[mid])

选B。A[mid] < p，A[mid] <= p错误，故39题不能选D。

43、⑤处应填 ( )
A. A[i].x == A[j].x
B. A[i].id < A[j].id
C. A[i].x == A[j].x && A[i].id < A[j].id
D. A[i].x < A[j].x && A[i].y < A[j].y

选D。

参考网站视频

2021CSP-J1
上一篇:
LaTeX常用公式
下一篇:
第1章 计算机网络概述

    • Copyright © 2023 - now SleepWalker | Powered by Hexo | Theme Bamboo

    本站总访问量： 次 |